说明:计算机中的最小存储单位为位(bit),一个字节(byte)占8位。
原码、反码、补码是计算机中对数字对二进制表示方法。
原码: 最高位作为符号位(0表示正数,1表示负数),非符号位为该数字绝对值对二进制表示。
如:
127的原码为 [0111 1111]
-127的原码为 [1111 1111]
反码: 正数反码与原码一致;负数,符号位不变,其余各位取反,则得到这个数字都反码表示形式。
如:
127的反码为[0111 1111]
-127的反码为[1000 0000]
补码: 正数的补码与原码一致;负数的补码是该数的反码加1
如:
127的补码为[0111 1111]
-127的补码为[1000 0001]
移码: 移码是在补码的基础上,符号位取反
如:
127的移码为[1111 1111]
-127的移码为[0000 0001]
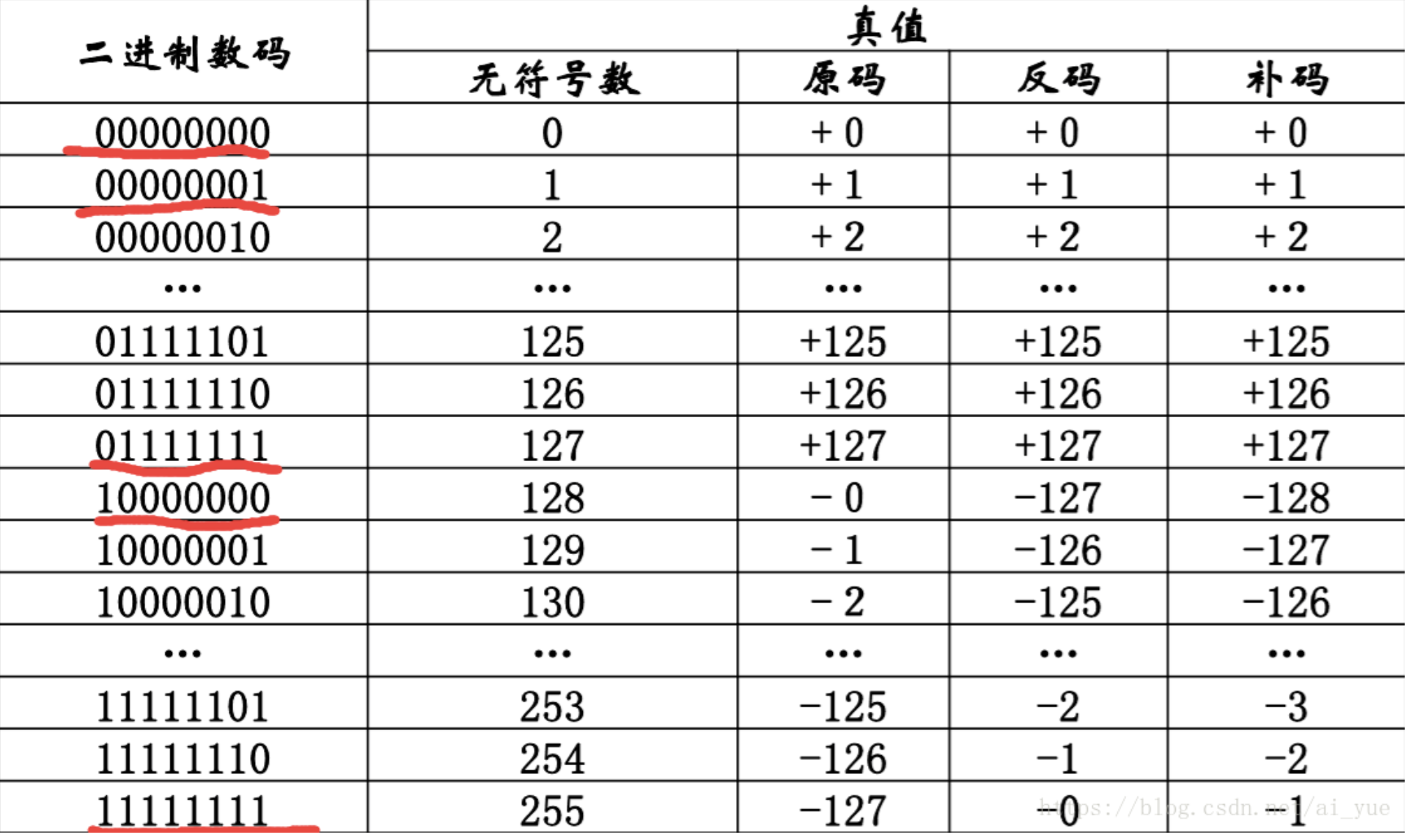
详情见下表:
| 数值 | 原码 | 反码 | 补码 | 移码 |
|---|---|---|---|---|
| 127 | 0111 1111 | 0111 1111 | 0111 1111 | 1111 1111 |
| -127 | 1111 1111 | 1000 0000 | 1000 0001 | 0000 0001 |
补充
- 计算机中的运算均是基于补码的。
- java中四个整数类型均采用二进制的补码表示
接下来以byte说明,为什么采用二进制补码表示数值范围。
byte占8个bit位,如果采用原码表示正整数(含0),范围为0-255,即2^8=256,一共256种状态,从全0到全1的各种排序组合。如果要表示负数,则符号位要占用一位(最高位 0表示正数,1表示负数),因此其绝对值最大范围为0-127,即2^7=128,一共正负各128种状态,即 -127到-0和0到127,这样总体上一个字节只有255种状态,因为0具有正0负0之分,显然浪费来一个编码。因此人们想到了另一种编码把负0利用起来,即当遇到负数时,采用补码来表示就可以解决这个问题,而遇到正数或0时还是用原码表示。因此这个负0通过补码算法处理后用来表示-128,这样一个字节的数值范围为-128-127,为256种状态。